表达式树的定义与后缀表达式构造表达式树

发表于 | 分类于

表达式树基础知识

表达式树是一类树，其基本结构为所有的叶节点为操作树，非叶节点为操作符。如下图所示为一种表达式树：

表达式树

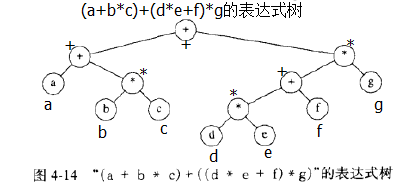
对于二元操作符，其形成的操作树是一种二叉树。对二叉表达式树进行不同的遍历得到不同的的表达式，当进行前序遍历时，得到的表达式称为前缀表达式，如上图前缀表达式为++a*bc*+*defg；当进行中序遍历时，得到的表达式称为中缀表达式，也就是日常书写习惯的的表达式，上图中最表达式为(a+(b*c))+(((d*e)+f)*g)；当进行后序遍历时，得到的表达式为后缀表达式（又称逆波兰表示法），这种形式的表达式可以直接由栈结构实现计算，上图后缀表达式为abc*+de*f+g*+。

后缀表达式构造表达式树

给出一组后缀表达式，要求构造出一颗表达式。由于后缀表达式树是后序遍历得到的，根节点的访问是在左右子树的访问顺序之后，因此后缀表达式序列第一个操作符和前面两个操作数（第一个操作符之前两个数一定是操作数）的三个节点一定可以组合成一颗三节点表达式树，通过如此递归构建便可以完成整棵数的构建，基本思路如下：

1. 读取符号序列，如果符号是操作数则新建一个节点的数并将地址压入栈中
2. 如果符号是操作符，则新建一个以该符号为元素的节点后从栈中弹出两个元素分别作为左右子树然后压入栈中。

后缀表达式构建表达式树实现

根据上节的分析，为了方便，采用单字符表示数字与操作符，实现代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
struct TreeNode
{
	char data;
	TreeNode *left;
	TreeNode *right;
	TreeNode(char inData): data(inData), left(nullptr), right(nullptr) {}
};

//true-操作符,false-操作数
bool isOperator(char inCh)
{
	if (inCh >= 'a' && inCh <= 'z') {
		return false;	
	}
	return true;
}


TreeNode *BuildExpressionTree(const char *inExpression)
{
	if (inExpression == nullptr || *inExpression == '\0') {
		return nullptr;
	}
	const char *cycleIter = inExpression;
	stack<TreeNode *> treeStack;
	while (*cycleIter != '\0') {
		if (!isOperator(*cycleIter)) {
			TreeNode *newNode = new TreeNode(*cycleIter);
			treeStack.push(newNode);
		}
		else {
			TreeNode *newNode = new TreeNode(*cycleIter);
			newNode->right = treeStack.top(); treeStack.pop();
			newNode->left = treeStack.top(); treeStack.pop();
			treeStack.push(newNode);
		}
		++cycleIter;
	}
	return treeStack.top();
}