二叉树的前序遍历、中序遍历、后序遍历的递归实现以及非递归实现

发表于 | 分类于

二叉树遍历的基本原理

先上一张前、中、后序遍历的路径图：图片来源

二叉树遍历流程图

如上图二叉树的遍历结果为：

  • 前序遍历为：ABDEFGC
  • 中序遍历为：DBFEGAC
  • 后序遍历为：DFGEBCA

由于树的定义是递归定义，因此自然而然遍历思路也是从递归遍历入手。二叉树的递归定义如下：

  1. 二叉树是由n个有限节点构成的集合
  2. n=0时为空树，n>0时二叉树由两个互不相交的的左右子树组成
  3. 左右子树也是一颗二叉树

二叉树的存储方式有链式存储和顺序存储，在链式存储中，除了保存数据外，需要两个指针分别指向左子树根节点和右子树根节点（有时为了方便会增加指向父节点的指针），基本结构如下：

1
2
3
4
5
6
7
8
9
template <typename DataType>
struct TreeNode
{
	DataType data; //存储的数据
	TreeNode *left; //指向左子树根节点
	TreeNode *right; //指向右子树根节点
	//TreeNode * parent; /*指向父节点，如果需要的话*/
	TreeNode(DataType inData): data(inData), right(nullptr), left(nullptr) {}
};

在顺序存储中，二叉树节点的存储顺序为由上到下、由左到右的顺序，顺序存储主要用来存储满二叉树或完全二叉树，和顺序存储有关的排序有堆排序。在顺序存储中，父节点与子节点有如下关系：

  • 下标从1开始，如果父节点下标为i，则左子节点的下标为2i，右子节点的下标为2i+1
  • 下标从0开始，如果父节点下标为i，则左子节点的下标为2i+1，右子节点的下标为2i+2

对于一个层数为k的二叉树，如果采用顺序存储的方式，则至少需要2k-1个存储单元，因此对于非满二叉树或者非完全二叉树有许多存储单元被浪费。

广义而言，二叉树的每一个节点都为根节点。二叉树的遍历主要是指采用链式存储方式下的遍历，由于二叉树的递归定义，最简单的遍历算法采用递归遍历，基本结构如下所示：

1
2
3
4
5
6
7
8
9
10
11
12
13
template <typename DataType>
void Traverse(TreeNode<DataType> * inNode)
{
	if (inNode == nullptr) {
		return;
	}
	//cout << inNode->data << ";"; /*如果在这里访问即为先序遍历*/
	Traverse(inNode->left);
	//cout << inNode->data << ";"; /*如果在这里访问即为中序遍历*/
	Traverse(inNode->right);
	//cout << inNode->data << ";"; /*如果在这里访问即为后序遍历*/
	return;
}
  • 先序遍历又称为先根遍历，可以理解为先访问根节点，再递归先序遍历左子树，最后先序遍历右子树
  • 中序遍历又可称为中根遍历，可以理解为中间再访问根节点，因此访问顺序是先中序遍历左子树，接着访问根节点，最后中序访问右子树
  • 后序遍历又可称为后根遍历，可以理解为根节点最后访问，因此访问顺序是先后序遍历左子树，接着后序遍历右子树，最后访问根节点
  • 层序遍历，是一种层次遍历，逐层遍历，每一层从左到右到右的顺序，该遍历方式需要借助于辅助空间（队列）

下图为遍历时的递归栈：

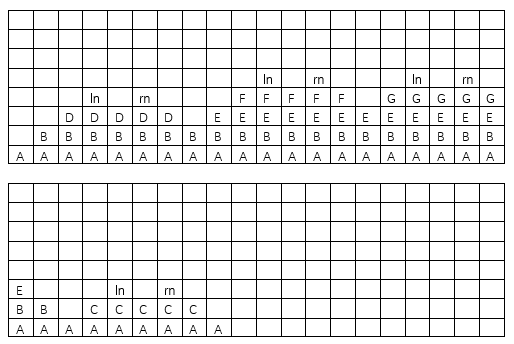
遍历时的递归栈

上图中ln代表左子节点为空指针，rn代表右子节点为空。如图所示，先序遍历就是第一次遇到节点时便输出，中序遍历则是第二次遇到时输出，既是上图中凹点处（左右两边栈高度均比当前栈高），后序遍历则是在栈即将该节点弹出时（最后一次访问）输出。

非递归实现遍历

  • 二叉树前序与中序遍历的非递归实现

非递归意味着无法让编译器帮助我们通过递归函数调用压栈和函数返回的方式记忆遍历线路，因此需要使用辅助栈空间来模拟函数调用返回过程。我们结合开始pou的图分析二叉树递归遍历的特点：首先访问左子树直到最左，然后再返回访问右子节点，再重复访问右子节点的左子树直到最左，因此我们在编写非递归实现时，可按照以下步骤来进行

1. 不断访问某一结的左子节点并压栈直到最左子节点
2. 弹出最后一个节点，访问该节点的右子节点并压入栈
3. 以该右子节点作为下一轮访问起点（根节点），重复1、2步

在递归遍历中，前序遍历是在将左子节点压栈之前输出，中序遍历是在节点的全部左子节点压入栈之后返回压入右子节点之前访问

上述思路的代码表现如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
#include <stack>
using std::stack;

template <typename DataType>
void NonRecursiveTraverse(TreeNode<DataType> * inNode)
{
	stack<TreeNode<DataType> *> nodeStack;
	TreeNode<DataType> *cycleNode = inNode;
	while (inNode != nullptr || !nodeStack.empty()) {
		//不断访问某一结的左子节点并压栈直到最左子节点
		while (cycleNode != nullptr) {
			//cout << cycleNode->data << ";"; /*在此处访问即为先序遍历*/
			nodeStack.push(cycleNode);
			cycleNode = cycleNode->left;
		}
		//到这里说明所有左子节点全部入栈
		//弹出最后一个节点，访问该节点的右子节点并作为下一轮遍历根节点
		if (!nodeStack.empty()) {
			cycleNode = nodeStack.top();
			//在此处访问即为中序遍历，时机为压入右子节点之前
			//cout << cycleNode->data << ";";
			//以该右子节点作为下一轮访问起点，重复外层while
			cycleNode = cycleNode->right;
			nodeStack.pop(); //立即弹出，否则不断访问同一个节点的右子树，形成死循环
		}
	}
}

在上述的代码中，压栈情况见下图：

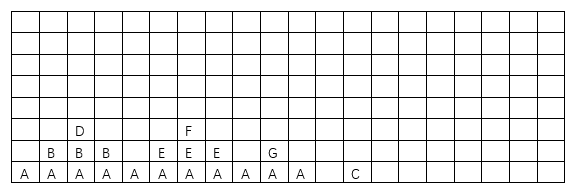
非递归压栈

由于辅助压栈，我们并没有将null压入栈中，如果发现左子节点为null则在保存右子节点地址后直接弹出该节点，并使用右子节点作为下一论访问起始节点，如果右子节点为null则表示该节点左右子树均遍历完毕，则继续弹出直至出现第一个右子树不为空的节点，重复递归。

压栈图中，在前序遍历时，只要遇到节点（压栈过程）就直接输出就可以保证根节点首先被输出，而中序遍历由于需要在左子树输出完毕后才能输出，因此只要保证在压栈返回时（出栈时）且准备遍历右子树时输出即可。

  • 二叉树后序遍历的非递归实现

根据递归遍历的调用栈，我们可以发现后序遍历在弹出栈之前输出即可完成后序遍历，在后序遍历中，由于需要先访问左右子节点后才能访问根节点，不能直接在上述代码中插入输出代码完成，因为在后序遍历中无法确定右子节点是否是叶节点或者已经访问过，因此需要保留访问标记，如果此时右子节点已经访问则可以输出当前右子节点的父节点

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
#include <stack>
using std::stack;

template <typename DataType>
void NonRecursivePostTraverse(TreeNode<DataType> * inNode)
{
	stack<TreeNode<DataType> *> nodeStack;
	TreeNode<DataType> *cycleNode = inNode;
	TreeNode<DataType> * hasCycle = nullptr; /*模拟递归调用返回点*/
	while (inNode != nullptr || !nodeStack.empty()) {
		/*不断访问某一结的左子节点并压栈直到最左子节点*/
		while (cycleNode != nullptr) {
			nodeStack.push(cycleNode);
			cycleNode = cycleNode->left;
		}

		//到这里说明所有左子节点全部入栈
		//弹出最后一个节点，访问该节点的右子节点并作为下一轮遍历根节点
		if (!nodeStack.empty()) {
			cycleNode = nodeStack.top();
        	        //如果右子节点为null，说明右子树已经遍历结束，可以输出根节点
			if (cycleNode->right == nullptr) {
				hasCycle = cycleNode; //保存已经访问的节点
				cout << cycleNode->data << ";";
				nodeStack.pop();
			}
			//如果右子节点已经访问，则也可以输出根节点
			else if (hasCycle == cycleNode->right) {
				hasCycle = cycleNode; //保存已经访问的节点
				cout << cycleNode->data << ";";
				nodeStack.pop();
			}
			//如果右子树还没有访问，则访问，否则置为nullptr继续出栈
			cycleNode = nullptr;
			if (!nodeStack.empty() && nodeStack.top()->right != hasCycle) {
				cycleNode = nodeStack.top()->right;
			}
		}
	}
}

根据上述代码，压栈情况下图：

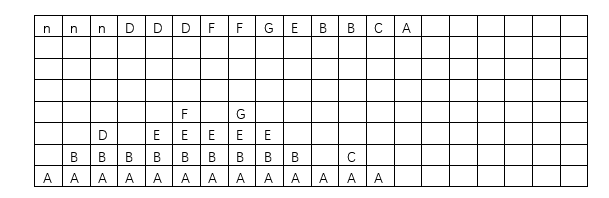
后序非递归压栈

最上面一行是当前保留的访问过的节点(n表示null节点)，由于右子节点被访问后该右子节点的父节点立刻可以被访问，因此只要发现右子树根节点被访问就可以立刻访问当前节点。

代码测试

简单地手动实现文中第一张图中的树，测试代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
#include <vector>
#include <random>
#include <ctime>
#include <iostream>
#include <algorithm>
#include <chrono>
#include <functional>
using namespace std;
using namespace chrono;

int main()
{
	TreeNode<char> testNode[7] = {'A', 'B', 'C', 'D', 'E', 'F', 'G'};

	testNode[0].left = &testNode[1];
	testNode[0].right = &testNode[2];

	testNode[1].left = &testNode[3];
	testNode[1].right = &testNode[4];

	testNode[4].left = &testNode[5];
	testNode[4].right = &testNode[6];

	auto startTime = system_clock::now();

	Traverse(testNode); /*调用具体的遍历算法*/

	auto endTime = system_clock::now();

	auto duration = duration_cast<microseconds>(endTime - startTime);
	cout << "TimeCost:" << duration.count() << endl;

	return 0;
}

参考

二叉树前序、中序、后序遍历非递归写法的透彻解析

二叉树前序、中序、后序遍历的迭代实现