前、后缀表达式重建表达式树的实现

发表于 | 分类于

前言

前、后缀表达式的基本含义可见本人的文章：传送门，本处不再赘述，表达式树在文中也有图示。针对只含有二元运算符的表达式树，树中所有的叶节点均为操作数，非叶节点均为操作符。前后缀表达式可以通过不同的遍历策略遍历表达式树得到，而通过前后缀表达式也可以重建得到表达式树，重建过程和二叉树的序列化与反序列化非常类似，由于操作树本身带有是叶子节点（无子节点）这一信息并且已知整棵树的根节点位置（中缀就无法直接得出根节点位置），因此可以直接根据表达式进行重建，各表达式的具体重建过程分析及代码实现见下文。

先声明本文将用到的基本数据结构：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
enum OperType
{
        /*OPERAND-操作数，OPERATOR-操作符*/
        OPERAND, OPERATOR
};

template <typename DataType>
union OperData {
        char operatorCh;
        DataType operand;
};

template <typename DataType>
struct ExpressionAtom
{
        OperType operFlag;
        OperData<DataType> operValue;
};

template <typename DataType>
struct TreeNode
{
        ExpressionAtom<DataType> nodeData;
        TreeNode<DataType> *left; /*左子节点*/
        TreeNode<DataType> *right; /*右子节点*/
        TreeNode() : left(nullptr), right(nullptr) {}
};

前缀表达式重建表达式树

由于二叉树是递归定义的，因此自然而然的思路就是尝试使用递归过程来重建二叉树，同时考虑到遍历过程也能通过辅助数据结构变成非递归过程，此时也可以考虑尝试使用非递归来重建，具体递归与非递归实现见下两小节。

前缀重建树的递归实现

由于前缀表达式的第一个节点是根节点，如果节点存在子节点，则紧邻其后的为其左子节点，否则需要递归返回，即本处递归终止条件是遇到操作数节点（因为操作数是没有子节点的）或者整个表达式重建完毕，具体实现思路可见代码及注释，代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
#include <vector>
using std::vector;

template <typename DataType>
TreeNode<DataType> *PrefixCore(vector<ExpressionAtom<DataType>> &inPrefix, int &index)
{
        if (index >= int(inPrefix.size())) {
                return nullptr;
        }
        TreeNode<DataType> *newNode = new TreeNode<DataType>; /*新建节点*/
        newNode->nodeData = inPrefix[index];

        /*由于前缀表达式先序遍历得到，先建立左子树，再建立右子树*/
        if (newNode->nodeData.operFlag != OPERAND) {
                newNode->left = PrefixCore(inPrefix, ++index);
                newNode->right = PrefixCore(inPrefix, ++index);
        }
        return newNode; /*返回新建立的节点*/
}

template <typename DataType>
TreeNode<DataType> *PrefixToExprTreeRecurve(vector<ExpressionAtom<DataType>> &inPrefix)
{
        if (inPrefix.size() <= 0) {
                return nullptr;
        }
        int index = 0;
        return PrefixCore(inPrefix, index);
}

前缀重建树的非递归实现

显然，如果需要不使用递归，则必须使用栈这种结构来保存中间结果。考虑到前序遍历的结果是根->左->右，因此我们可以反向遍历表达式，在遇到操作符时可以弹出栈中两个操作数（子表达式树看作一个操作数）和该操作符组成一颗子表达式树并把子表达式树根节点压入栈中，不断重复该过程直到栈中只剩下一个节点即为最终结果，具体实现可见如下代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
#include <vector>
#include <stack>
using std::vector;
using std::stack;

template <typename DataType>
TreeNode<DataType> *PrefixToExprTree(vector<ExpressionAtom<DataType>> &inPrefix)
{
        if (inPrefix.size()  <= 1) {
                return nullptr;
        }
        stack<TreeNode<DataType> *> nodeStack; /*放置节点指针*/
        for (int i = int(inPrefix.size())-1; i >= 0; i--) {
                TreeNode<DataType> *newNode = new TreeNode<DataType>; /*新建节点*/
                newNode->nodeData = inPrefix[i];
                /*遇到操作符弹出两个元素*/
                if (newNode->nodeData.operFlag == OPERATOR) {
                        TreeNode<DataType> *operand1 = nodeStack.top(); nodeStack.pop();
                        TreeNode<DataType> *operand2 = nodeStack.top(); nodeStack.pop();
                        /*组建子表达式树*/
                        newNode->left = operand1;
                        newNode->right = operand2;
                }
                nodeStack.push(newNode); /*节点入栈*/
        }
        /*返回栈顶元素*/
        return nodeStack.top();
}

前缀重建树代码测试

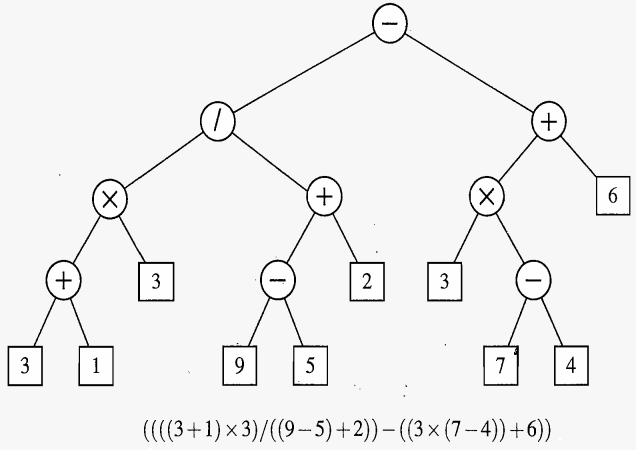
考虑使用本人前面测试用的表达式树，树的形态如下图所示：图片来源

表达式树

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
#include <iostream>
#include <vector>
using std::vector;
using std::cout;
using std::endl;

template <typename DataType>
bool isEqual(ExpressionAtom<DataType>&in1, ExpressionAtom<DataType>&in2)
{
	if (in1.operFlag == in2.operFlag) {
		if (in1.operFlag == OPERAND) {
			return in1.operValue.operand == in2.operValue.operand;
		}
		else {
			return in1.operValue.operatorCh == in2.operValue.operatorCh;
		}
	}
	return  false;
}

template <typename DataType>
void PrefixVisit(TreeNode<DataType> *root, vector<ExpressionAtom<DataType>> &result)
{
        if (root == nullptr) {
                return;
        }
        result.push_back(root->nodeData);

        PrefixVisit(root->left, result);
        PrefixVisit(root->right, result);
}

int main()
{
        vector<ExpressionAtom<int>> testVec;

        ExpressionAtom<int> manualData;

        manualData.operFlag = OPERATOR;
        manualData.operValue.operatorCh = '-';
        testVec.push_back(manualData);

        manualData.operFlag = OPERATOR;
        manualData.operValue.operatorCh = '/';
        testVec.push_back(manualData);

        manualData.operFlag = OPERATOR;
        manualData.operValue.operatorCh = '*';
        testVec.push_back(manualData);

        manualData.operFlag = OPERATOR;
        manualData.operValue.operatorCh = '+';
        testVec.push_back(manualData);

        manualData.operFlag = OPERAND;
        manualData.operValue.operand = 3;
        testVec.push_back(manualData);

        manualData.operFlag = OPERAND;
        manualData.operValue.operand = 1;
        testVec.push_back(manualData);

        manualData.operFlag = OPERAND;
        manualData.operValue.operand = 3;
        testVec.push_back(manualData);

        manualData.operFlag = OPERATOR;
        manualData.operValue.operatorCh = '+';
        testVec.push_back(manualData);

        manualData.operFlag = OPERATOR;
        manualData.operValue.operatorCh = '-';
        testVec.push_back(manualData);

        manualData.operFlag = OPERAND;
        manualData.operValue.operand = 9;
        testVec.push_back(manualData);

        manualData.operFlag = OPERAND;
        manualData.operValue.operand = 5;
        testVec.push_back(manualData);

        manualData.operFlag = OPERAND;
        manualData.operValue.operand = 2;
        testVec.push_back(manualData);

        manualData.operFlag = OPERATOR;
        manualData.operValue.operatorCh = '+';
        testVec.push_back(manualData);

        manualData.operFlag = OPERATOR;
        manualData.operValue.operatorCh = '*';
        testVec.push_back(manualData);

        manualData.operFlag = OPERAND;
        manualData.operValue.operand = 3;
        testVec.push_back(manualData);

        manualData.operFlag = OPERATOR;
        manualData.operValue.operatorCh = '-';
        testVec.push_back(manualData);

        manualData.operFlag = OPERAND;
        manualData.operValue.operand = 7;
        testVec.push_back(manualData);

        manualData.operFlag = OPERAND;
        manualData.operValue.operand = 4;
        testVec.push_back(manualData);

        manualData.operFlag = OPERAND;
        manualData.operValue.operand = 6;
        testVec.push_back(manualData);

        auto result = PrefixToExprTreeRecurve(testVec); /*调用相应的代码*/

        vector<ExpressionAtom<int>> resultVec;
        PrefixVisit(result, resultVec);

        bool correct = true;
	size_t i = 0;
	for (i = 0; i < resultVec.size() && testVec.size(); i++) {
		if (!isEqual(resultVec[i], testVec[i])) {
			correct = false; break;
		}
	}

	if (correct && i >= resultVec.size() && i >= testVec.size()) {
		cout << "Correct" << endl;
	}
	else {
		cout << "Wrong" << endl;
	}

        return 0;
}

后缀表达式重建表达式树

后缀表达式和前缀表达式的区别是后缀表达式的操作符是在操作数的后面，即左->右->根，因此后缀重建的递归算法可以参考前缀表达式重建算法，只需稍微改变遍历顺序即可。具体代码可见如下两小节。

后缀重建树的递归实现

正如前面所说，后缀前缀表达式不同在于根节点位置，对于后缀表达式根节点在最后，因此参考前缀表达式重建树的递归算法只需从后往前递归即可，基本实现代码如下所示：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
#include <vector>
using std::vector;

template <typename DataType>
TreeNode<DataType> *PostfixCore(vector<ExpressionAtom<DataType>> &inPostfix, int &index)
{
        if (index < 0) {
                return nullptr;
        }
        TreeNode<DataType> *newNode = new TreeNode<DataType>; /*新建节点*/
        newNode->nodeData = inPostfix[index];

        /*由于前缀遍历得到，先建立左子树，再建立右子树*/
        if (newNode->nodeData.operFlag != OPERAND) {
                newNode->right = PostfixCore(inPostfix, --index);
                newNode->left = PostfixCore(inPostfix, --index);
        }
        return newNode; /*返回新建立的节点*/
}

template <typename DataType>
TreeNode<DataType> *PostfixToExprTreeRecurve(vector<ExpressionAtom<DataType>> &inPostfix)
{
        if (inPostfix.size() <= 1) {
                return nullptr;
        }
        int index = int(inPostfix.size()) - 1;
        return PostfixCore(inPostfix, index);
}

后缀重建树的非递归实现

直接把后缀计算的代码稍作修改即可，代码如下所示：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
#include <vector>
#include <stack>
using std::vector;
using std::stack;

template <typename DataType>
TreeNode<DataType> *PostfixToExprTree(vector<ExpressionAtom<DataType>> &inPostfix)
{
        if (inPostfix.size()  <= 1) {
                return nullptr;
        }
        stack<TreeNode<DataType> *> nodeStack; /*放置根结点指针*/
        for (size_t i = 0; i < inPostfix.size(); i++) {
                TreeNode<DataType> *newNode = new TreeNode<DataType>; /*新建节点*/
                newNode->nodeData = inPostfix[i];
                if (newNode->nodeData.operFlag == OPERATOR) {
                        TreeNode<DataType> *operand1 = nodeStack.top(); nodeStack.pop();
                        TreeNode<DataType> *operand2 = nodeStack.top(); nodeStack.pop();
                        /*遇到操作符直接出栈两个操作数*/
                        newNode->left = operand2;
                        newNode->right = operand1;
                }
                nodeStack.push(newNode); /*操作数或者子表达式树入栈*/
        }
        /*返回栈顶元素*/
        return nodeStack.top();
}

后缀重建树代码测试

依旧使用前缀图中的表达式树，测试代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
#include <iostream>
#include <vector>
using std::vector;
using std::cout;
using std::endl;


template <typename DataType>
void PostfixVisit(TreeNode<DataType> *root, vector<ExpressionAtom<DataType>> &result)
{
        if (root == nullptr) {
                return;
        }
        PostfixVisit(root->left, result);
        PostfixVisit(root->right, result);
        result.push_back(root->nodeData);
}

int main()
{
        vector<ExpressionAtom<int>> testVec;

        ExpressionAtom<int> manualData;

        manualData.operFlag = OPERAND;
        manualData.operValue.operand = 3;
        testVec.push_back(manualData);

        manualData.operFlag = OPERAND;
        manualData.operValue.operand = 1;
        testVec.push_back(manualData);

        manualData.operFlag = OPERATOR;
        manualData.operValue.operatorCh = '+';
        testVec.push_back(manualData);

        manualData.operFlag = OPERAND;
        manualData.operValue.operand = 3;
        testVec.push_back(manualData);

        manualData.operFlag = OPERATOR;
        manualData.operValue.operatorCh = '*';
        testVec.push_back(manualData);

        manualData.operFlag = OPERAND;
        manualData.operValue.operand = 9;
        testVec.push_back(manualData);

        manualData.operFlag = OPERAND;
        manualData.operValue.operand = 5;
        testVec.push_back(manualData);

        manualData.operFlag = OPERATOR;
        manualData.operValue.operatorCh = '-';
        testVec.push_back(manualData);

        manualData.operFlag = OPERAND;
        manualData.operValue.operand = 2;
        testVec.push_back(manualData);

        manualData.operFlag = OPERATOR;
        manualData.operValue.operatorCh = '+';
        testVec.push_back(manualData);

        manualData.operFlag = OPERATOR;
        manualData.operValue.operatorCh = '/';
        testVec.push_back(manualData);

        manualData.operFlag = OPERAND;
        manualData.operValue.operand = 3;
        testVec.push_back(manualData);

        manualData.operFlag = OPERAND;
        manualData.operValue.operand = 7;
        testVec.push_back(manualData);

        manualData.operFlag = OPERAND;
        manualData.operValue.operand = 4;
        testVec.push_back(manualData);

        manualData.operFlag = OPERATOR;
        manualData.operValue.operatorCh = '-';
        testVec.push_back(manualData);

        manualData.operFlag = OPERATOR;
        manualData.operValue.operatorCh = '*';
        testVec.push_back(manualData);


        manualData.operFlag = OPERAND;
        manualData.operValue.operand = 6;
        testVec.push_back(manualData);

        manualData.operFlag = OPERATOR;
        manualData.operValue.operatorCh = '+';
        testVec.push_back(manualData);

        manualData.operFlag = OPERATOR;
        manualData.operValue.operatorCh = '-';
        testVec.push_back(manualData);

        auto result = PostfixToExprTreeRecurve(testVec); /*调用具体的函数*/

        vector<ExpressionAtom<int>> resultVec;
        PostfixVisit(result, resultVec);

        bool correct = true;
	size_t i = 0;
	for (i = 0; i < resultVec.size() && testVec.size(); i++) {
		if (!isEqual(resultVec[i], testVec[i])) {
			correct = false; break;
		}
	}

	if (correct && i >= resultVec.size() && i >= testVec.size()) {
		cout << "Correct" << endl;
	}
	else {
		cout << "Wrong" << endl;
	}

        return 0;
}

参考资料

数据结构

根据表达式序列构建表达式树