前言
前缀表达式又称波兰表达式,其将操作符放置于操作数前面,该类型的表达式无需括号仍然可以无歧义地被解析,如果将表达式以表达式树的形式展现,则前缀表达式对应于前序遍历结果。
中缀表达式在表达式中将操作符(双目)置于操作数的中间,是目前常用的一种表示方法,中缀表达式需要通过括号来指示运算优先顺序,一般中缀表达式在计算机中无法直接用于计算,中缀表达式对应于表达式树的中序遍历结果。
后缀表达式又称逆波兰表达式,式中操作符位于操作数的后面,在计算机内部易于直接计算(借助栈),和前缀表达式一样后缀表达式也无需借助括号便可以无歧地被解析,后缀表达式对应于表达式树的后序遍历结果。
本文分别实现将前缀、中缀表达式转变为后缀表达式并且实现一个简单的后缀表达式计算器。同时约定放置表达式的基本数据结构如下:
1 | enum OperType |
注:本文所指表达式操作符只含有双目运算符且运算符的结合顺序为从左到右。
前缀转后缀表达式
我们可以通过观察前缀和后缀表达式在表达式树中的遍历顺序:前缀,根->左->右;后缀,左->右->根。从以上顺序可以得出两者遍历顺序中操作数始终在一起,只是操作符顺序不一致。而且在表达式树上操作数都是叶子节点而操作符必定有两个(双目)子节点。因此在实现前缀转后缀时只需把根放在操作符之后即可,而操作数相对顺序保持不变。综合以上分析我们可以用一个栈来存放根(操作符),队列用来存放结果,通过队列+栈实现根的逆序,基本实现代码如下:
1 |
|
前缀转后缀代码测试
使用如下图所示表达式树生成的前缀表达式来进行测试:图片来源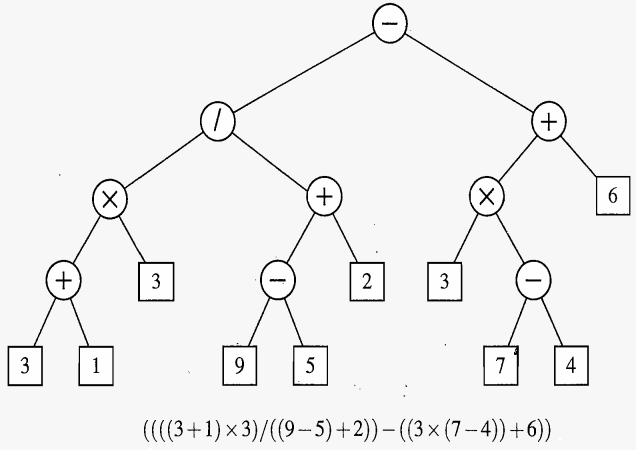
1 |
|
中缀转后缀表达式
表达式树在进行中序遍历时,为了保留求值顺序信息必须通过增加括号,因此在进行中缀转后缀时必须处理括号的情况。中缀表达式转后缀表达式有一个经典的调度场算法,具体可参见参考资料中的文章。由于考虑到栈的先进后出的特性,而且表达式从左到右结合,因此操作数在后缀表达式中的相对顺序不发生变化。在决定操作符的输出顺序时只要保证高优先级先出栈即可。综合上述可以使用一个栈来保存操作符,如果当前读到的操作符优先级大于栈顶操作符则一直压栈直至优先级小于等于栈顶操作符。在处理括号时,一旦出现左括号则先压入栈,出现右括号则不断从操作符栈中弹出直至遇到左括号为止。具体实现代码如下:
1 |
|
中缀转后缀代码测试
使用前缀中的表达式树,同时使用括号改变优先级,具体测试代码如下:
1 |
|
后缀表达式求值
后缀表达式求值非常简单,只要在遇到操作符后立刻弹出两个操作数(双目运算符)进行计算。最后栈里剩下一个元素即为求值结果,具体见下所示:
1 |
|
后缀表达式求值代码测试
在进行测试时直接使用上节求出的后缀表达式,具体代码如下:
1 |
|