数据结构之树基础

发表于 | 分类于

树的递归定义

树由于其结构特点，一般采用递归定义的方式，其定义方式如下：

  • 一棵树是一些节点的集合
  • 集合可以为空集；若非空则称一棵树由称为根的节点以及 0 个或多个非空的互不相交的子树$T_1,T_2,….T_k$组成
  • 子树中每一棵的根都被来自根 $r$ 的一条有向边所连接

树相关概念

  • 树叶

没有儿子的节点称为树叶

  • 路径

节点 $n_1$ 到 $n_k$ 的路径定义为节点 $n_1,n_2….n_k$ 的一个序列，使得节点 $n_i$ 是 $n_{i+1}$ 的父节点，路径长为该路径上边的长，即 $k-1$。

  • 深度

对于任意节点 $n_i$， $n_i$ 的深度为从根到 $n_i$ 唯一路径的长。

  • 内部路径长

一棵树所有节点的深度的称为内部路径长

  • 树的高

$n_i$ 的高为 $n_i$ 到一片树叶最长的路径长

  • 节点的度

节点所拥有的子树的个数称为该节点的度。

  • 树的度

节点的度中最大值被称为树的度

  • 森林

零棵或者有限棵不相交的树的集合称为森林

  • 兄弟节点

具有相同父节点的节点互称为兄弟节点

树的实现

由于树子节点的个数是不确定的，因此通过保存每个子节点的指针是非常不合理的。目前树的存储结构大致存在以下几种。

  • 父节点表示法

由于除了根没有父节点以外，所有节点有且只有一个父节点，通过存储父节点信息的数据域来表示树即是父节点表示法的基本思路，数据结构如下：

1
2
3
4
5
6
template <typename DataType, typename PositionType>
struct TreeNode
{
	DataType data; //数据
	PositionType parent; //父节点位置
};
  • 孩子表示法

父节点表示法中子节点可以快速找到自己的父节点，但是父节点难以查找自己的子节点，因此孩子表示法的思路是存储子节点的位置信息，数据结构如下：

1
2
3
4
5
6
template <typename DataType, typename PositionType>
struct TreeNode
{
	DataType data; //数据
	list<PositionType> child; //保存所有子节点位置
};
  • 双亲孩子表示法

孩子表示法虽然解决了查找子节点的问题，但是子节点查找父节点又变得困难，因此可以结合父节点表示法和孩子表示法的优点，由此有双亲孩子表示法，数据结构如下：

1
2
3
4
5
6
7
template <typename DataType, typename PositionType>
struct TreeNode
{
	DataType data; //数据
	PositionType parent; //父节点位置
	list<PositionType> child; //保存所有子节点位置
};
  • 孩子兄弟表示法（又称树的二叉链表实现方式）

根据树的定义，树确定以后，从左到右的子节点顺序也确定下来了，也就是父节点第一个子节点也确定了，而每个子节点最接近的右兄弟节点也确定下来了，由此引出孩子兄弟表示法，基本数据结构如下所示：

1
2
3
4
5
6
7
template <typename DataType, typename PositionType>
struct TreeNode
{
	DataType data; //数据
	PositionType firstChild; //第一个子节点
	PositionType nextSibling; //当前节点最近右兄弟节点
};

二叉树基础

  • 二叉树具有五种基本的形态

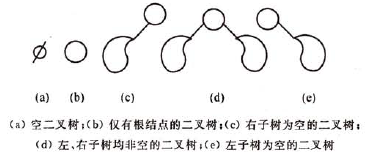
由于二叉树分为左右子树，因此有五种基本形态：1）空树，2）仅含有根节点，3）右子树为空，4）左子树为空，5）左右子树非空。如下示意图所示：图片来源

二叉树五种形态

  • 二叉树第 $i(i>=1)$ 层至多有 $2^{i-1}$ 个节点

由于每个节点可以有两个子节点，故下一层节点数目最多是上一层的两倍，从根节点往前递推便可得到该值。

  • 深度为 $k(k>=1)$ 的二叉树最多含有 $2^k-1$ 个节点

由每层最多含有的节点数可有 $\sum_{i=1}^{k}2^{i-1}=2^k-1$。等比数列求和

  • 任意一棵二叉树，如果含有 $n_0$ 个叶子节点以及 $n_2$ 个度为2的节点，则有 $n_0=n_2+1$

由于二叉树总结点数n等于树中边数量+1，则假设度为1的节点数量为 $n_1$，则有如下关系：$n=n_0+n_1+n_2=2n_2+n_1+1$，可得出如上结论。

  • 满二叉树

一棵深度为 $k(k>=1)$ 的二叉树且有 $2^k-1$ 个节点，则称为满二叉树。

  • 完全二叉树

完全二叉树的定义需要借助于满二叉树：假设对满二叉树按照从上至下、从左到右的顺序进行编号，则对于一颗深度为 $k(k>=1)$ 和节点数为 $n$ 的二叉树，当且仅当每一个节点都与深度为 $k(k>=1)$ 满二叉树编号一一对应则称为完全二叉树。可以认为完全二叉树是指将满二叉树从最底层从右到左删除节点形成的一棵二叉树，其叶节点只会出现在倒数一、二层。完全二叉树可以使用顺序存储的方式，其双亲结点和子节点下标具有固定的关系。

  • 具有 $n$ 个节点的完全二叉树深度为 $\lfloor log_2n \rfloor + 1$。

假设完全二叉树的深度为 $k$，则根据深度节点数量关系有 $2^{k-1}-1<n<=2^{k}-1$，化简可得。

树的种类

  • 无序树：树中任意节点的子节点之间没有顺序关系

  • 有序树：树中任意节点的子节点之间有顺序关系，有序树可分为：

    • 二叉树
      • 完全二叉树
      • 平衡二叉树（AVL树、红黑树、伸展树、Treap、加权平衡树、AA树、替罪羊树、节点大小平衡树）
      • 排序二叉树（二叉查找树）
    • 霍夫曼树
    • 平衡树
      • 2-3树
    • B树
      • B树
      • B+树
      • B*树
    • Trie树

树的遍历

树的遍历方式有多种，按照处理节点的顺序可以分为如下几种

  • 先序遍历（又称为前序遍历、先根遍历）

在先序遍历中，对节点的处理是在处理子节点之前处理的。

  • 后序遍历（又称为后根遍历）

在后序遍历中，对节点的处理是在处理子节点之后处理的。

  • 中序遍历（又称为中根遍历）

中序遍历一般是二叉树中的概念，中序遍历的节点处理顺序是先处理左子节点，然后处理本节点，最后处理右子节点。

  • 层序遍历（BFS）

层序遍历是指从根开始，每次依次从左到右处理该层节点。

先序遍历、后序遍历、中序遍历均属于深度优先遍历，层序遍历属于广度优先遍历。

参考资料

数据结构中各种树

数据结构