优先队列的定义与二叉堆实现

发表于 | 分类于

优先队列基础

优先队列是指一种数据结构，其每个元素都有各自的优先级，出队顺序由元素的优先级决定。优先队列一般使用堆来实现。优先队列一般至少需要支持如下操作：

  1. 插入带优先级的元素
  2. 取出最高优先级的元素
  3. 查看最高优先级的元素

优先队列有多种实现方式，分别简述如下：

  1. 无序顺序表：在表尾插入，删除时遍历找到优先级最高的元素，因此插入时间复杂度O(1)而删除O(n)
  2. 无序链表：在头节点插入，删除时时遍历找到优先级最高的元素，因此插入时间复杂度O(1)而删除O(n)
  3. 有序线性表：保持插入后的线性表有序，因此插入时间复杂度O(n)，删除时间复杂度O(1)
  4. 有序链表：保持插入后的线性表有序，因此插入时间复杂度O(n)，删除时间复杂度O(1)
  5. 二叉查找树：插入操作O(log2n)，而删除时间复杂度也为O(log2n)
  6. 二叉堆：插入与删除均为O(log2n)，构造时间复杂度为O(n)

二叉堆基础知识

二叉堆有两个性质，即结构性和堆序性。结构性是指二叉堆是一棵完全被填满的二叉树，只在底层存在例外，即倒数第二层也可能存在叶节点。而堆序性是指对于每一个节点X，X的父亲中的关键字小于（或等于）X中的关键字（根节点除外）。由于堆序性的原因，在插入和删除节点后需要调整二叉堆使得其保持堆序性。在插入时，可以先将带插入的节点放入下一个空闲位置，然后采用称为上滤策略的二叉堆调整方法，不断和父节点比较，如果不满足堆序性就交换，直到满足堆序性或者成为根节点。而删除最小元时，先把堆中最后一个元素填入原来最小元素的空穴，然后采用称为下滤的策略调整二叉堆，其不断和左右子节点比较，和较小的子节点交换，不断重复该过程直到满足堆序性为止。

二叉堆的实现

根据上节的分析，二叉堆主要有如下操作：

  • 插入或者称为入队：Enqueue
  • 删除或者说称为出队：Dequeue
  • 查看当前队首元素（即最小元素）：Front
  • 清空队列：MakeEmpty
  • 建立二叉堆：BuildHeap

在STL中，优先队列priority_queue底层采用vector实现，优先队列定义如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
template <typename DataType>
class PriorityQueue
{
public:
	PriorityQueue(int inSize);
	~PriorityQueue();
	void Enqueue(DataType inData);
	void Dequeue();
	DataType Front();
	bool isEmpty();
	void MakeEmpty();
	int QueueSize();
	void BuildHeap(vector<DataType> &inArray);
private:
	int capacity;
	int queueSize;
	DataType *queuePtr;
};

如上所示，数据成员主要有二叉堆容量，二叉堆大小以及二叉堆实际元素指针，采用动态分配的方式，以下依次实现各函数（最小堆）。

  • 构造函数，初始化空间并设置数据成员初始值
1
2
3
4
5
template <typename DataType>
PriorityQueue<DataType>::PriorityQueue(int inSize):capacity(inSize), queueSize(0),queuePtr(nullptr)
{
	queuePtr = new DataType[inSize];
}
  • 入队函数，采用上滤策略调整二叉堆，如果堆已满则抛出异常
1
2
3
4
5
6
7
8
9
10
11
12
13
template <typename DataType>
void PriorityQueue<DataType>::Enqueue(DataType inData)
{
	if (queueSize >= capacity) {
		throw "Priority queue is full!";
	}
	int i = queueSize;
	while (i > 0 && inData < queuePtr[(i-1)/2]) {
		queuePtr[i] = queuePtr[(i-1)/2];
		i= (i-1)/2;
	}
	queuePtr[i] = inData; ++queueSize;
}
  • 出队函数，采用下滤策略调整二叉堆
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
template <typename DataType>
void PriorityQueue<DataType>::Dequeue()
{
	if (queueSize <= 0) {
		throw "Priority queue is empty!";
	}
	DataType lastElement =  queuePtr[queueSize-1];
	int i = 0;
	for (i = 0; 2*i+1 < queueSize;) {
		int minChild = 2*i+1;
		if (minChild+1 < queueSize && queuePtr[minChild] > queuePtr[minChild+1]) {
			minChild += 1;
		}
		if (lastElement > queuePtr[minChild]) {
			queuePtr[i] = queuePtr[minChild];
			i = minChild;
		}
		else {
			break;
		}
	}
	queuePtr[i] = lastElement; --queueSize;
}
  • 查看队首元素
1
2
3
4
5
6
7
8
template <typename DataType>
DataType PriorityQueue<DataType>::Front()
{
	if (queueSize <= 0) {
		throw "Priority queue is empty!";
	}
	return queuePtr[0];
}
  • 判断是否为空
1
2
3
4
5
template <typename DataType>
bool PriorityQueue<DataType>::isEmpty()
{
	return queueSize <= 0;
}
  • 清空优先队列
1
2
3
4
5
template <typename DataType>
void PriorityQueue<DataType>::MakeEmpty()
{
	queueSize = 0;
}
  • 返回优先队列大小
1
2
3
4
5
template <typename DataType>
int PriorityQueue<DataType>::QueueSize()
{
	return queueSize;
}

  • 建堆，可以直接循环调用Enqueue函数（时间复杂度O(N)），本文采用另外一种方法，算法思路如下：

    二叉堆的左右子树也是一个二叉堆，因此从最后一个非叶节点开始，调整该子树成为二叉堆，依次往前推进，循环调整直到根节点即完成二叉堆的构建。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
template <typename DataType>
void PriorityQueue<DataType>::BuildHeap(vector<DataType> &inArray)
{
	if (inArray.size() > capacity) {
		throw "Out of space!";
	}
	queueSize = 0;
	for (size_t i = 0; i < inArray.size(); i++) {
		queuePtr[queueSize++] = inArray.at(i);
	}
	for (int i = (queueSize-1)/2; i >= 0; i--) {
		int tmpElement = queuePtr[i];
		int j = i;
		while (2*j+1 < queueSize) {
			int miniChild = 2*j+1;
			if (miniChild+1 < queueSize && queuePtr[miniChild] > queuePtr[miniChild+1]) {
				miniChild += 1;
			}
			if (tmpElement > queuePtr[miniChild]) {
				queuePtr[j] = queuePtr[miniChild];
				j = miniChild;
			}
			else {
				break;
			}
		}
		queuePtr[j] = tmpElement;
	}
}
  • 析构函数，释放内存
1
2
3
4
5
6
7
template <typename DataType>
PriorityQueue<DataType>::~PriorityQueue()
{
	MakeEmpty();
	delete [] queuePtr; 
	queuePtr = nullptr;
}

二叉堆除了上述操作以外，还可以有降低某位置关键字的值，增加某位置关键字的值以及删除某个位置的关键字，各操作的基本思路如下：

  • 降低某位置关键字值：采用上滤（最小堆）策略调整二叉堆使其保持堆序性
  • 增加某位置关键字的值：采用下滤策略（最小堆）策略调整二叉堆使其保持堆序性
  • 删除某个位置的关键字：将该位置值设为比最小值还小（最小堆），然后上滤并调用出队函数即可
  • 合并：调用插入函数依次插入

二叉堆的相关定理

  • 包含2h+1个节点高为h的理想二叉树的节点的高度的和为2h+1-1-(h+1)

证明：根据二叉树的定义，在高为h的层上总共有1个节点，高为h-1的曾是上有1*2个节点，即每层节点个数是上一层的两倍，故高为h-i层节点数量为2i个。则所有节点高的和为∑i=0~h2i*(h-i)。求解该式便可得出上述结论。将h=logN代入便可得出建堆的时间复杂度为O(N)

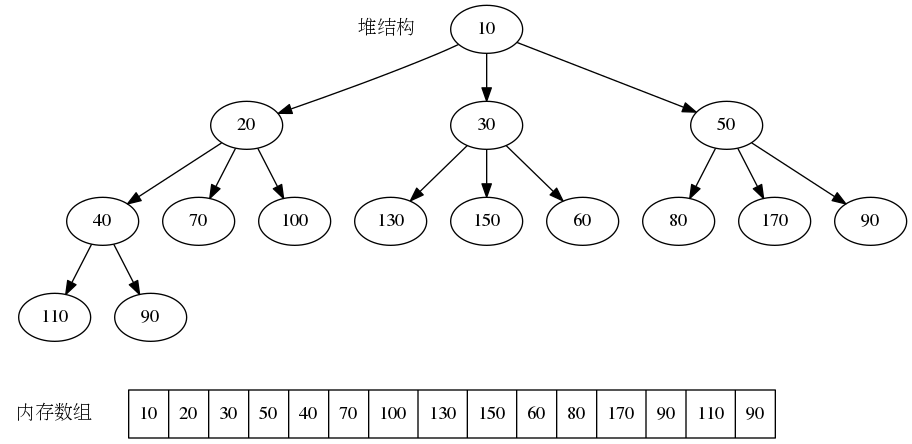
二叉堆扩展-d堆

d堆是二叉堆的简单推广，其节点有d个子节点，因此二叉堆是d=2的情况。d堆由于子节点数多，其高度比较浅，插入操作时间复杂度为O(logdN)，删除时间复杂度为dO(logdN)。下图为一个3-堆。图片来源

3堆