数据结构之左式堆的定义与实现

发表于 | 分类于

左式堆基础知识

左式堆又称为左高树、左偏堆、左倾堆、左偏树，是一种二叉树。左式堆和二叉堆一样也具有结构性和堆序性，但是和二叉堆不同的是，左式堆不是理想平衡的而且趋于非常不平衡。左式堆是一种非常方便进行合并的堆，二叉堆是一种特殊的左式堆。

左式堆的性质

  • 节点的键值小于或等于左右子节点
  • 任意节点X，左子节点零路径长至少与右子节点零路径长相等，即左子节点零路径长大于等于左子节点零路径长
  • 节点的零路径长为右子节点零路径长加1
  • 一颗N节点左式堆root节点零路径长最多为log(N+1)-1
  • 在右路径上有r个节点的左式堆必然至少有2r-1个节点
  • N个节点的左式堆有一条右路径最多含有log(N+1)个节点

左式堆的某节点X的重量W(X)为以X为根的内部节点的数量。WE(X)=W(左子树)+W右子树+1。该值可以递归计算。

零路径长（null path length）是指从节点X到没有两个字节点的最短路径长，因此具有0个或者1个子结点的零路径长为0。左式堆的性质使得树向左进一步加深。如下图为零路径长示意图，节点内数值为零路径长。图片来源

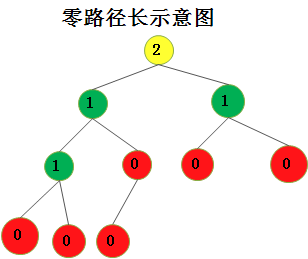
零路径长示意图

根据左式堆的定义，左式堆的左右子树依然是一个左式堆。

左式堆的基本操作

二叉堆的基本操作有插入和删除，而左式堆的基本操作为合并，左式堆的插入是合并的一种特例（单节点左式堆合并），删除看成将左式堆分解成两个左式堆再进行合并操作。左式堆在进行合并时，除了需要保证堆序性外（父节点小于等于子节点值），还需要保证合并后的树依然是一个左式堆，因此合并过程是一个递归过程，描述如下：

  1. 如果有一个堆为空，则返回另外一个左式堆
  2. 比较两个左式堆根的大小，以小值根作为新左式堆的根，另外一个左式堆和小根堆的右子树合并
  3. 调整新树使得满足零路径长要求
  4. 递归上述三个过程

左式堆的实现

由于左式堆最重要的操作是合并，其余操作均可以通过调用合并操作完成，因此左式堆有如下操作：

  • 返回最小值：FindMin
  • 合并两个左式堆:Merge
  • 删除最小值（出队）:DeleteMin
  • 插入一个节点：InsertElement

根据《数据结构与算法分析-C语言描述》一书的定义，左式堆定义如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
template <typename DataType>
struct Node
{
	DataType data;
	Node *left;
	Node *right;
	int nullPathLength;
	Node(DataType inData):data(inData), left(nullptr), right(nullptr), nullPathLength(0) {} 
};


template <typename DataType>
class LeftistHeap
{
public:
	LeftistHeap(): root(nullptr) {}
	~LeftistHeap();
	DataType FindMin();
	void Merge(Node<DataType> *inTree);
	void DeleteMin();
	void InsertElement(DataType inElement);
	bool IsEmpty();
	void MakeEmpty();
private:
	Node<DataType> *MergeCore(Node<DataType> *inTree1, Node<DataType> *inTree2);
	Node<DataType> *root;
};

如上所示节点数据结构中新增了一个表示零路径长的成员，其余和二叉树的定义相同，以下分别实现各函数。

  • 查找最小元素，如果左式堆为空则抛出异常
1
2
3
4
5
6
7
8
template <typename DataType>
DataType LeftistHeap<DataType>::FindMin()
{
	if (root == nullptr) {
		throw "Leftist heap is empty!";
	}
	return root->data;
}
  • 合并两棵左式堆核心函数
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
template <typename DataType>
Node<DataType> * LeftistHeap<DataType>::MergeCore(Node<DataType> *inTree1, Node<DataType> *inTree2)
{
	if (inTree1 == nullptr) {
		return inTree2;
	}

	if (inTree2 == nullptr) {
		return inTree1;
	}
	if (inTree1->data > inTree2->data) {
		swap(inTree1, inTree2); //STL库函数
	}
	if (inTree1->left == nullptr) {
		inTree1->left = inTree2;
	}
	else {
		inTree1->right = MergeCore(inTree1->right, inTree2);
		if (inTree1->left->nullPathLength < inTree1->right->nullPathLength) {
			swap(inTree1->left, inTree1->right);
		}
		inTree1->nullPathLength = inTree1->right->nullPathLength+1;
	}
	return inTree1;
}
  • 合并两棵左式堆
1
2
3
4
5
template <typename DataType>
void LeftistHeap<DataType>::Merge(Node<DataType> *inTree)
{
	root = MergeCore(root, inTree);
}
  • 删除最小元素，拆解为左右两棵子树，然后调用合并函数进行合并
1
2
3
4
5
6
7
template <typename DataType>
void LeftistHeap<DataType>::DeleteMin()
{
	Node<DataType> *tmp = root;
	root = MergeCore(root->left, root->right);
	delete tmp;
}
  • 插入，转变为单节点左式堆的合并
1
2
3
4
5
6
template <typename DataType>
void LeftistHeap<DataType>::InsertElement(DataType inElement)
{
	Node<DataType> *newNode = new Node<DataType>(inElement);
	root = MergeCore(root, newNode);
}
  • 判断左式堆是否为空
1
2
3
4
5
template <typename DataType>
bool LeftistHeap<DataType>::IsEmpty()
{
	return root == nullptr;
}
  • 清空左式堆，采用非递归中序遍历清空
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
template <typename DataType>
void LeftistHeap<DataType>::MakeEmpty()
{
	if (root == nullptr) {
		return;
	}
	Node<DataType> *cycleIter = root;
	stack<Node<DataType> *> nodeStack;
	while (cycleIter != nullptr || !nodeStack.empty()) {
		while (cycleIter != nullptr) {
			nodeStack.push(cycleIter);
			cycleIter = cycleIter->left;
		}
		if (!nodeStack.empty()) {
			Node<DataType> *tmp = nodeStack.top();
			cycleIter = tmp->right;
			delete tmp; nodeStack.pop();
		}
	}
	root = nullptr;
}
  • 析构函数，回收内存
1
2
3
4
5
template <typename DataType>
LeftistHeap<DataType>::~LeftistHeap()
{
	MakeEmpty();
}

在测试时，只要把图中左式堆的插入顺序根据二叉树的中序遍历的序列输入即可。从大量数据构造左式堆时可以先构造n个单元素的队列，然后删除队列里的前两个元素合并，并把合并结果放入队尾，重复删除合并过程直到队列只有一个元素。

在非递归实现合并时，分两趟完成，第一趟将两棵树右路径上的节点分离并按照大小排序，然后依次将分离的右节点连按顺序连接，第二趟调整左右子节点使树满足零路径长条件。

参考文章

结构之美——优先队列基本结构（四）——二叉堆、d堆、左式堆、斜堆

优先队列——左式堆

左式堆的实现与详解