数据结构之二项队列的定义与实现

二项队列基础知识

二项队列不是一棵堆序的树，而是堆序树的集合，称为森林。堆序树中的每一棵树叫着二项式树，高度为0的二项树是一棵单节点树，高度为k的二项树B_k的树通过将一棵二项树B_k-1附接到另一棵B_k-1的根上构成，如下图所示为二项式树：图片来源

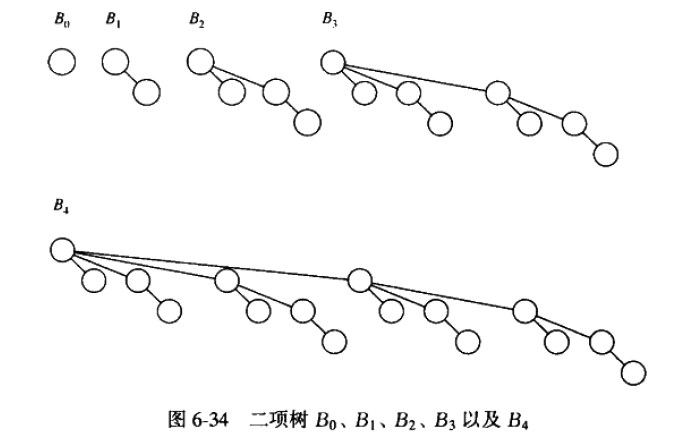
每项棵的节点个数按照高从0到k二进制表示为(1)(10)(100)(1000)(10000)…..

二项树的递归定义如下：

• 度为0的二项树只有一个节点
• 度数为k的二项树有一个根节点，根节点下有k个子女，每个子女度数分别为k-1、k-2…..2、1、0的二项树的根

度数为k（或者说高度为k）的二项式树一共有2^k个节点，深度为d处节点是二项式系数（k/d）组合中的C(k,d)。一棵二叉树的秩为从为从根节点开始到其叶节点中最长的一条树链上结点的个数。

二项队列的操作

按照二项队列的定义，二项队列中的每棵树为堆序树，因此最小元素可以通过遍历所有树的根节点来得到。由于对于N个节点的二项队列总共有logN棵不同的树,因此通常查找时间复杂度为O(logN)。对于合并操作，只要存在相同度的二项式树，就把根节点值较大的一颗成为根节点值较小二项树根的子树，合并操作最坏时间复杂度为O(logN)。插入操作和左式堆类似，可以转化为合并操作，即单节点二项树的合并，最坏时间复杂度O(logN)。删除操作也类似，删除后二项树分裂成二项队列，此时只需和原始二项队列合并即可，最坏时间复杂度O(logN)。总而言之，二项式队列的操作最终都可以采用合并操作完成，和左式堆非常类似。一般而言，对于一个初始为空的二项队列进行N次插入最坏时间复杂度为O(N)。

下图为队列H1和H2的合并过程：图片来源

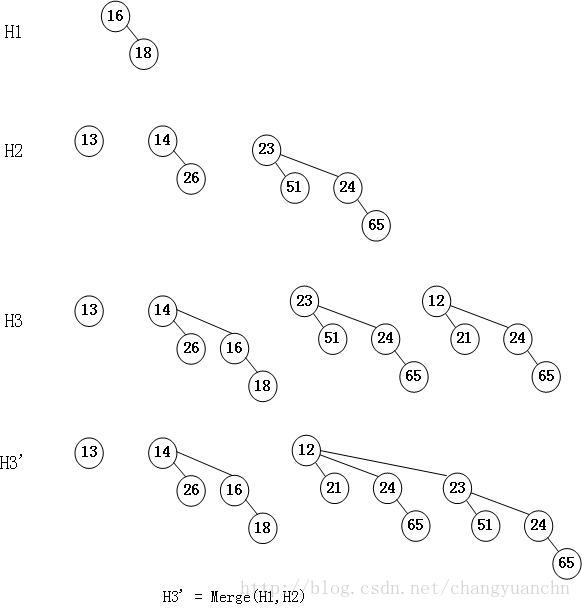
合并过程类似于二进制加法。

二项队列的实现

根据二项式树的特点，其一个节点可能有多个子节点，因此在存储时可能需要采用孩子兄弟表示法来存储。而且子节点按照子树的节点数量从大到小排序，如下图所示：图片来源

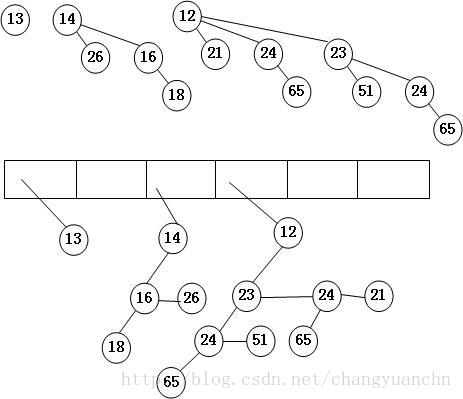
二项树合并图解：

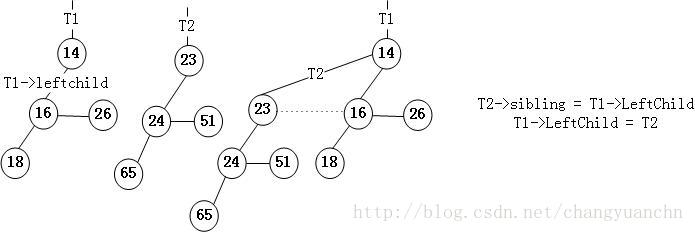
二项队列的操作主要有：

• 合并：Merge
• 删除最小值：DeleteMin
• 插入节点：InsertElement
• 清空二项队列：MakeEmpty
• 查找最小元素：FindMin

根据以上分析，有如下数据结构定义：

template <typename DataType>
struct Node
{
	DataType data;
	Node * leftChild;
	Node * nextSibling;
	Node() : data(-1), leftChild(nullptr), nextSibling(nullptr) {}
};

template <typename DataType>
class BinomialQueue
{
public:
	BinomialQueue(int inCapacity);
	~BinomialQueue();
	void Merge(BinomialQueue<DataType> &otherQueue);
	void DeleteMin();
	void InsertElement(DataType inElement);
	void MakeEmpty();
	DataType FindMin();
private:
	Node<DataType> *MergeCore(Node<DataType> *inTree1, Node<DataType> *inTree2);
	int capacity; //此处容量是指可以容纳树的数量
	int currentSize; //当前容纳树度数最高+1
	Node<DataType> **queue;
};

以下分别实现各函数

• 构造函数，根据输入最大容量建立二项队列，动态分配

template <typename DataType>
BinomialQueue<DataType>::BinomialQueue(int inCapacity) : capacity(inCapacity), currentSize(0), queue(nullptr)
{
	queue = new Node<DataType> *[inCapacity];
	for (int i = 0; i < inCapacity; i++) {
		queue[i] = nullptr;
	}
}

• 合并核心函数，即切换指针操作

template <typename DataType>
Node<DataType> *BinomialQueue<DataType>::MergeCore(Node<DataType> *inTree1, Node<DataType> *inTree2)
{
	if (inTree1 == nullptr) return inTree2;
	if (inTree2 == nullptr) return inTree1;
	if (inTree1->data > inTree2->data) swap(inTree1, inTree2);

	inTree2->nextSibling = inTree1->leftChild;
	inTree1->leftChild = inTree2;
	return inTree1;
}

• 合并函数，采用笨办法而不是《数据结构与算法分析-C语言描述》一书中非常巧妙的办法，分2*2*2=8种情况讨论

template <typename DataType>
void BinomialQueue<DataType>::Merge(BinomialQueue<DataType> &otherQueue)
{
	int maxSize = currentSize > otherQueue.currentSize ? currentSize : otherQueue.currentSize;
	Node<DataType> *carry = nullptr;
	Node<DataType> *tree1 = nullptr, *tree2 = nullptr; 
	for (int i = 0; i < maxSize+1; i++) {
		tree1 = queue[i]; tree2 = otherQueue.queue[i];
		if (carry == nullptr) {
			if (tree1 != nullptr && tree2 != nullptr) {
				carry = MergeCore(tree1, tree2);
				queue[i] =  otherQueue.queue[i] = nullptr;
			}
			else {
				queue[i] = tree1 != nullptr ? tree1 :tree2;
				otherQueue.queue[i] = nullptr;
			}
		}
		else {
			if (tree1 != nullptr && tree2 != nullptr) {
				queue[i] = carry;
				carry = MergeCore(tree1, tree2);
				otherQueue.queue[i] = nullptr;
			}
			else if (tree1 == nullptr && tree2 == nullptr){
				queue[i] = carry;
			}
			else {
				tree1 = tree1 != nullptr ? tree1 : tree2;
				carry = MergeCore(tree1, carry);
				queue[i] =  otherQueue.queue[i] = nullptr;
			}
		}
	}
	if (queue[currentSize] != nullptr) ++currentSize;
}

• 删除最小元素，先遍历找到最小元素然后删除根几点，将剩下的子树组成一个新的二项队列然后调用合并函数

template <typename DataType>
void BinomialQueue<DataType>::DeleteMin()
{
	DataType minElement = numeric_limits<DataType>::max(); //库函数，当前类型最大值
	int miniTreeIndex = -1;
	for (int i = 0; i < currentSize; i++) {
		if (queue[i] != nullptr && minElement > queue[i]->data) {
			miniTreeIndex = i; minElement = queue[i]->data;
		}
	}
	if (miniTreeIndex == -1) throw "Queue is empty!"; //没有元素
	
	BinomialQueue<DataType> remainQueue(currentSize+5); 
	remainQueue.currentSize = miniTreeIndex;
	Node<DataType> *startTree = queue[miniTreeIndex]->leftChild;
	for (int i = miniTreeIndex-1; i >= 0; --i) {
		remainQueue.queue[i] = startTree;
		startTree = startTree->nextSibling;
		remainQueue.queue[i]->nextSibling = nullptr;
	}
	delete queue[miniTreeIndex]; queue[miniTreeIndex] = nullptr;
	Merge(remainQueue);
}

• 插入元素，新建一个单树队列，调用Merge函数

template <typename DataType>
void BinomialQueue<DataType>::InsertElement(DataType inElement)
{
	BinomialQueue<DataType> remainQueue(currentSize+5); 
	remainQueue.queue[0] = new Node<DataType>;
	remainQueue.queue[0]->data = inElement;
	remainQueue.currentSize = 1;
	Merge(remainQueue);
}

• 清空二项式队列，非递归遍历，采用类似于二叉树中序遍历的方式

template <typename DataType>
void BinomialQueue<DataType>::MakeEmpty()
{
	for (int i = 0; i < currentSize; i++) {
		stack<Node<DataType> *> nodeStack;
		Node<DataType> *cycleIter = queue[i];
		while (cycleIter != nullptr || !nodeStack.empty()) {
			while (cycleIter != nullptr) {
				nodeStack.push(cycleIter); cycleIter = cycleIter->leftChild;
			}
			if (!nodeStack.empty()) {
				Node<DataType> *tmp = nodeStack.top();
				nodeStack.pop();
				cycleIter = tmp->nextSibling;
				delete tmp;
			}
		}
	}
	for (int i = 0; i < currentSize; i++) {
		queue[i] = nullptr;
	}
	currentSize = 0;
}

• 查找最小元素

template <typename DataType>
DataType BinomialQueue<DataType>::FindMin()
{
	DataType minElement = numeric_limits<DataType>::max(); //库函数，当前类型最大值
	int miniTreeIndex = -1;
	for (int i = 0; i < currentSize; i++) {
		if (queue[i] != nullptr && minElement > queue[i]->data) {
			miniTreeIndex = i; minElement = queue[i]->data;
		}
	}
	if (miniTreeIndex == -1) throw "Queue is empty!"; //没有元素
	return minElement;
}

• 析构函数，清空内存

template <typename DataType>
BinomialQueue<DataType>::~BinomialQueue()
{
	MakeEmpty(); delete [] queue;
}

参考文章

二项队列

二项堆(一)之图文解析和C语言的实现