二叉树的非递归前、中、后、层序遍历的不同实现

发表于 | 分类于

前言

由于二叉树是一种递归定义的数据结构，采用递归的方式去遍历是一种非常简洁方便的做法，但是如果要求使用非递归的方式去遍历整棵二叉树则必须使用辅助的空间。以下分别实现二叉树的前序、中序、后序以及层序的遍历算法。约定二叉树的基本结构如下：

1
2
3
4
5
6
7
8
template <typename DataType>
struct TreeNode
{
	DataType data; //存储的数据
	TreeNode *left; /*指向左子树根节点*/
	TreeNode *right; /*指向右子树根节点*/
	TreeNode(DataType inData): data(inData), right(nullptr), left(nullptr) {}
};

前序非递归遍历

前序遍历的顺序为根->左->右，因此在使用辅助栈时，结合栈的先进后出特性，为了让左子树能在右子树之前弹出，我们可以先把右子节点先压入栈中，然后就可以保证左子节点先弹出，实现代码如下所示：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
#include <stack>
using std::stack;

template <typename DataType>
vector<DataType> PreorderTraverse(TreeNode<DataType> *root)
{
        vector<DataType> result;
        if (root == nullptr) {
                return result;
        }

        stack<TreeNode<DataType> *> nodeStack;
        nodeStack.push(root);
        while (!nodeStack.empty()) {
                /*弹出根节点并访问之*/
                TreeNode<DataType> *tmp = nodeStack.top();
                result.push_back(tmp->data);
                nodeStack.pop();

                /*先压右子节点再压左子节点*/
                if (tmp->right != nullptr) {
                        nodeStack.push(tmp->right);
                }
                if (tmp->left != nullptr) {
                        nodeStack.push(tmp->left);
                }
        }
        return result;
}

中序非递归遍历

中序遍历的顺序为左->根->右，因此在左子树被访问前根才能被访问，因此需要一直压栈最左，然后弹栈压入栈顶的右子节点，代码实现如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
#include <stack>
using std::stack;

template <typename DataType>
vector<DataType> InorderTraverse(TreeNode<DataType> *root)
{
        vector<DataType> result;
        if (root == nullptr) {
                return result;
        }

        stack<TreeNode<DataType> *> nodeStack;
        TreeNode<DataType> *cycleIter = root;
        while (cycleIter != nullptr || !nodeStack.empty()) {
                /*一直压左子节点*/
                if (cycleIter != nullptr) {
                        nodeStack.push(cycleIter);
                        cycleIter = cycleIter->left;
                }
                else {
                        /*压到最左了*/
                        result.push_back(nodeStack.top()->data);
                        cycleIter = nodeStack.top()->right;
                        nodeStack.pop();
                }
        }
        return result;
}

后序非递归遍历

后序遍历的顺序为左->右->根，由于根是最后访问，我们可以考虑前序遍历的思路，最后镜像结果即可。后序遍历的镜像访问顺序为根->右->左，和前序遍历的顺序只是访问左右的结果不同，因此可以将前序代码稍作调整即可用于后序遍历，代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
#include <stack>
#include <algorithm>
using std::stack;

template <typename DataType>
vector<DataType> PostorderTraverse(TreeNode<DataType> *root)
{
        vector<DataType> result;
        if (root == nullptr) {
                return result;
        }

        stack<TreeNode<DataType> *> nodeStack;
        nodeStack.push(root);
        while (!nodeStack.empty()) {
                /*弹出根节点并访问之*/
                TreeNode<DataType> *tmp = nodeStack.top();
                result.push_back(tmp->data);
                nodeStack.pop();

                /*和前序相反*/
                if (tmp->left != nullptr) {
                        nodeStack.push(tmp->left);
                }
                if (tmp->right != nullptr) {
                        nodeStack.push(tmp->right);
                }
        }
        reverse(result.begin(), result.end());
        return result;
}

层序遍历

层序遍历类似于广度优先搜索(BFS)，此时一般使用队列来辅助存储，其思路可以借鉴前序遍历思路，只是弹出(出队)顺序略有不同，只需对前序代码稍作修改即可，具体代码见下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
#include <queue>
using std::queue;

template <typename DataType>
vector<DataType> BFSTraverse(TreeNode<DataType> *root)
{
        vector<DataType> result;
        if (root == nullptr) {
                return result;
        }

        queue<TreeNode<DataType> *> nodeQueue;
        nodeQueue.push(root);
        while (!nodeQueue.empty()) {
                /*弹出根节点并访问之*/
                TreeNode<DataType> *tmp = nodeQueue.front();
                result.push_back(tmp->data);
                nodeQueue.pop();

                /*先压左子节点再压右子节点*/
                if (tmp->left != nullptr) {
                        nodeQueue.push(tmp->left);
                }
                if (tmp->right != nullptr) {
                        nodeQueue.push(tmp->right);
                }

        }
        return result;
}

如果要考虑分层输出的问题，则需要增加几个标识变量用来标识某一层的结束。由于已知第一层只有一个根节点，通过这个已知条件就可以推算下一层结束节点，换句话来说是一层最后的一个节点的右子节点是下一层的最后一个节点。将上述层序代码稍作变形就可以得到支持分层的代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
#include <queue>
using std::queue;

template <typename DataType>
vector<vector<DataType>> BFSTraverseWithLevel(TreeNode<DataType> *root)
{
        vector<vector<DataType>> result;
        if (root == nullptr) {
                return result;
        }

        queue<TreeNode<DataType> *> nodeQueue;
        TreeNode<DataType> *lastNode = root;
        TreeNode<DataType> *nextLevelLastNode = nullptr;
        nodeQueue.push(root);
        vector<DataType> oneLevelData;
        while (!nodeQueue.empty()) {
                /*弹出根节点并访问之*/
                TreeNode<DataType> *tmp = nodeQueue.front();
                oneLevelData.push_back(tmp->data);
                nodeQueue.pop();

                /*先压左子节点再压右子节点*/
                if (tmp->left != nullptr) {
                        nodeQueue.push(tmp->left);
                        nextLevelLastNode = tmp->left;
                }
                if (tmp->right != nullptr) {
                        nodeQueue.push(tmp->right);
                        nextLevelLastNode = tmp->right;
                }
                if (tmp == lastNode) {
                        result.push_back(oneLevelData);
                        oneLevelData.clear();
                        lastNode = nextLevelLastNode;
                }

        }
        return result;
}

代码测试

手动做出如下图的一棵二叉树：图片来源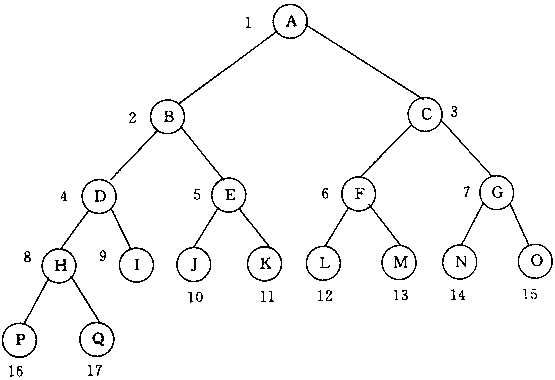
二叉树测试案例

测试代码如下所示：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
#include <vector>
#include <random>
#include <ctime>
#include <iostream>
#include <algorithm>
#include <chrono>
#include <functional>
using namespace std;
using namespace chrono;

int main()
{
	TreeNode<char> testNode[17] = {'A', 'B', 'C', 'D', 'E',
                                       'F', 'G', 'H', 'I', 'J',
                                       'K', 'L', 'M', 'N', 'O',
                                       'P', 'Q'};

	testNode[0].left = &testNode[1];
	testNode[0].right = &testNode[2];

	testNode[1].left = &testNode[3];
	testNode[1].right = &testNode[4];

        testNode[2].left = &testNode[5];
	testNode[2].right = &testNode[6];

        testNode[3].left = &testNode[7];
	testNode[3].right = &testNode[8];

	testNode[4].left = &testNode[9];
	testNode[4].right = &testNode[10];

        testNode[5].left = &testNode[11];
	testNode[5].right = &testNode[12];

        testNode[6].left = &testNode[13];
	testNode[6].right = &testNode[14];

        testNode[7].left = &testNode[15];
	testNode[7].right = &testNode[16];



        cout << "---------------前序--------------" << endl;

        auto startTime = system_clock::now();

	vector<char> result1 = PreorderTraverse(testNode);

        auto endTime = system_clock::now();

        for (size_t i = 0; i < result1.size(); i++) {
                cout << result1[i] << ";";
        }
        cout << endl;

        auto duration = duration_cast<microseconds>(endTime - startTime);
	cout << "TimeCost:" << duration.count() << endl;

        cout << "---------------中序--------------" << endl;

        startTime = system_clock::now();

	vector<char> result2 = InorderTraverse(testNode);

        endTime = system_clock::now();

        for (size_t i = 0; i < result2.size(); i++) {
                cout << result2[i] << ";";
        }
        cout << endl;

        duration = duration_cast<microseconds>(endTime - startTime);
	cout << "TimeCost:" << duration.count() << endl;

        cout << "---------------后序--------------" << endl;

        startTime = system_clock::now();

	vector<char> result3 = PostorderTraverse(testNode);

        endTime = system_clock::now();

        for (size_t i = 0; i < result3.size(); i++) {
                cout << result3[i] << ";";
        }
        cout << endl;

        duration = duration_cast<microseconds>(endTime - startTime);
	cout << "TimeCost:" << duration.count() << endl;

        cout << "---------------层序--------------" << endl;

        startTime = system_clock::now();

	vector<char> result4 = BFSTraverse(testNode);

        endTime = system_clock::now();

        for (size_t i = 0; i < result4.size(); i++) {
                cout << result4[i] << ";";
        }
        cout << endl;

        duration = duration_cast<microseconds>(endTime - startTime);
	cout << "TimeCost:" << duration.count() << endl;

        cout << "---------------层序（分层）--------------" << endl;

        startTime = system_clock::now();

	vector<vector<char>> result5 = BFSTraverseWithLevel(testNode);

        endTime = system_clock::now();

        for (size_t i = 0; i < result5.size(); i++) {
                for (size_t j = 0; j < result5[i].size(); j++) {
                        cout << result5[i][j] << ";";
                }
                cout << endl;
        }

        duration = duration_cast<microseconds>(endTime - startTime);
	cout << "TimeCost:" << duration.count() << endl;

	return 0;
}

参考文章

二叉树遍历之非递归算法

更简单的非递归遍历二叉树的方法

广度优先搜索